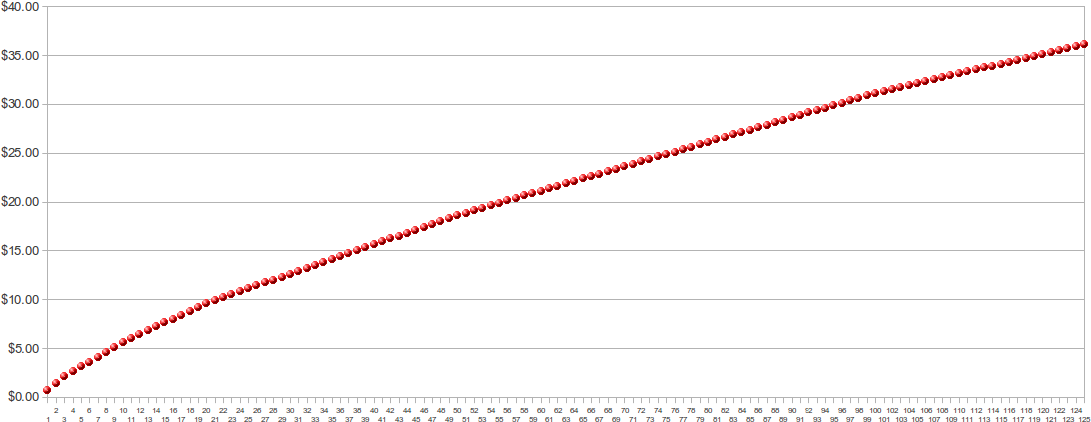
Tabelas de preços de impressão são interessantes. É muito comum que quanto mais você imprima mais baratas as impressões fiquem, fazendo com que o gráfico de preço por impressões não seja monótono (isso é, você não necessariamente pague mais por um número maior de impressões).

Isso torna as gráficas boas candidatas de lugares para pensar em gráficos de funções de primeiro grau, assim como a busca binária é uma boa candidata de aplicação para pensar sobre logaritmos.

Hoje fui imprimir uma partitura e me deparei com a seguinte tabela:

(registrada em uma foto de um bilhão de dólares)

Se desenharmos um gráfico de preço (eixo y — vertical) por número de impressões (eixo x — horizontal), temos:

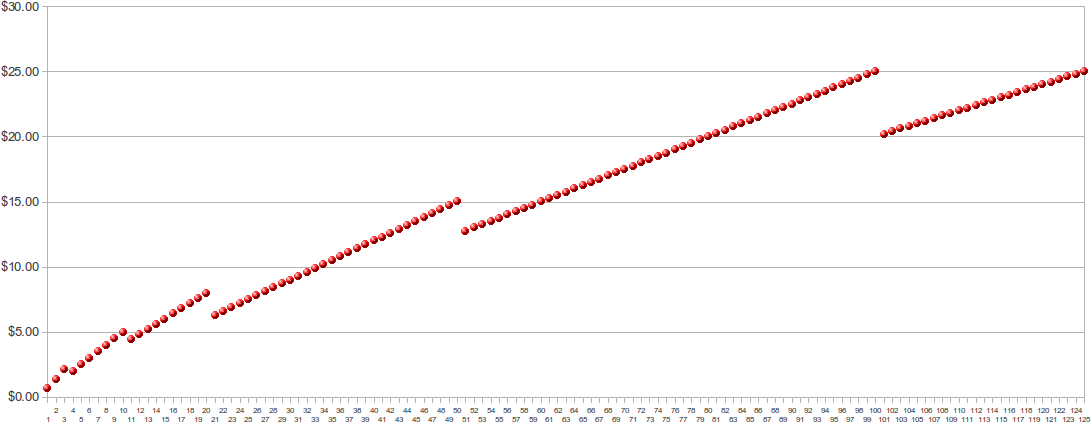
Observando esse gráfico (feio), percebemos que há alguns números de impressões que economicamente não faz sentido fazer. Por exemplo, 3 impressões custam R$ 2,10 enquanto 4 impressões custam R$ 2,00. 20 impressões custam R$ 8,00 enquanto 21 impressões custam R$ 6,30. 100 impressões custam R$ 25,00 enquanto 101 impressões custam R$ 20,20.

Mas não só esses. Os valores que não faz sentido imprimir no gráfico são todos aqueles cujo existe algum ponto a direita na mesma altura ou mais baixo, ou seja, todos os que pintei de amarelo:

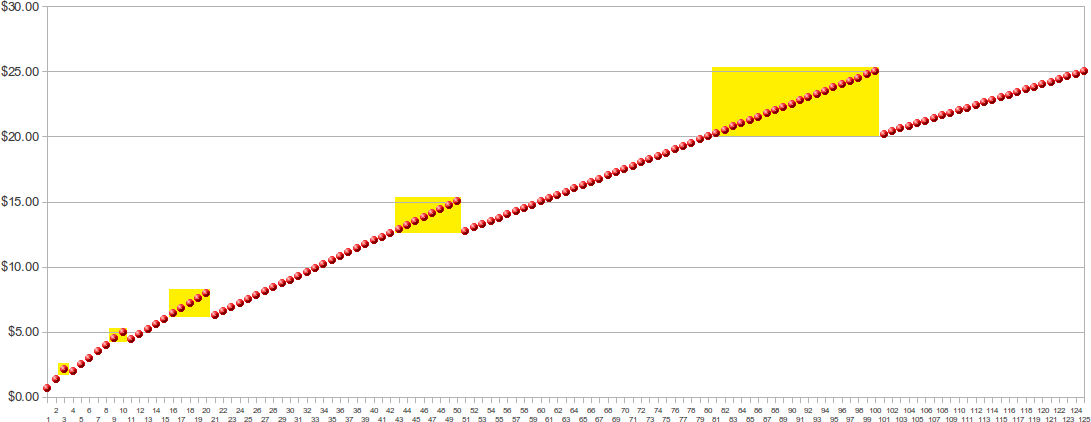
Um problema econômico interessante para quando se está numa gráfica imprimindo é, portanto, descobrir quando estamos nos pontos amarelos. É interessante porque, se estivermos nos pontos amarelos, podemos aproveitar para imprimir mais cópias ou pedir ao dono da gráfica um desconto. Afinal, é razoável esperar que o preço que a gente pague seja limitado por este gráfico:

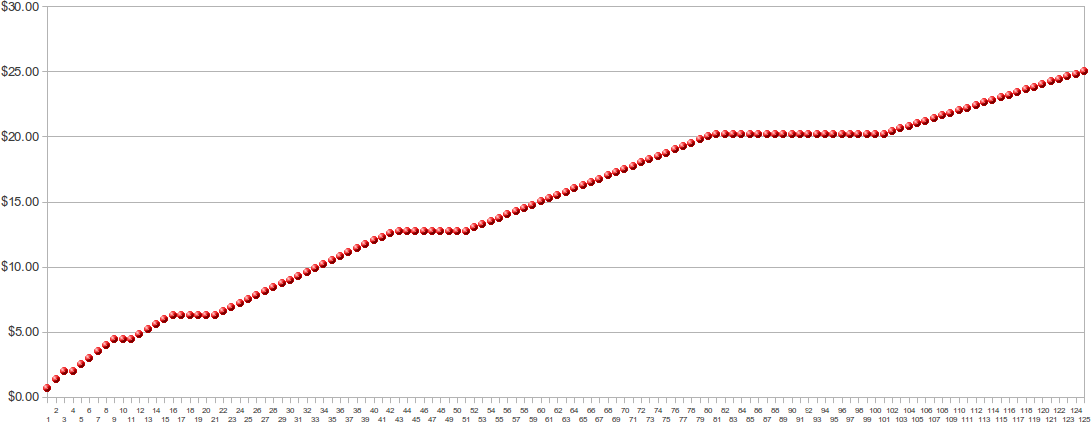
Descobrir se estamos numa região amarela é simples. Basta calcular o preço que pagaríamos a princípio (multiplicar o número de cópias pelo preço por cópias da região em que estamos) e comparar com o preço que pagaríamos se pedíssemos o menor número de cópias da região imediatamente mais barata. Por exemplo, faz sentido imprimir 15 cópias porque $15 \times 0.40=6.00$ é menor do que $21 \times 0.30 = 6.30$, mas não faz sentido imprimir 85 cópias porque $85 \times 0.25 = 21.25$ é maior do que $101 \times 0.20 = 20.20$.

Agora vamos inverter o problema. Vamos supôr que você é a gráfica e quer evitar esse tipo de cliente insuportável, fazendo o preço ir ficando mais barato proporcionalmente com o número de impressões, mas mantendo a função monótona (crescendo).

Poderíamos pensar em funções que crescem cada vez mais devagar…

… mas parece complicado achar uma função que não nos dê prejuízo quando o cliente quiser muitas cópias e parece especialmente complicado explicar para o cliente que o preço de x cópias é um monte de constantes multiplicadas pelo logaritmo de x.

Então talvez seja melhor pensar em funções de primeiro grau mesmo.

Se você separar todas as funções que encontramos na tabela de preços do problema anterior e colocá-las num gráfico, você vai ver que a interseção delas só acontece num ponto: o ponto x = 0.

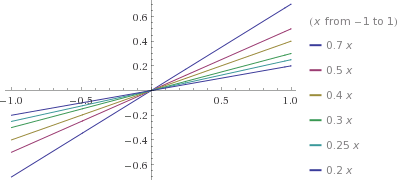
(esse gráfico foi um oferecimento Wolfram Alpha)

Uma forma de resolver o problema é fazer com que as interseções sejam nos pontos onde o preço das impressões muda. Isso se faz movendo cada uma das funções um pouquinho pra cima, isso é, adicionando constantes às funções de primeiro grau.

Por exemplo: 3 cópias custam R$ 2,10. Se a partir de 4 cópias quisermos que as cópias custem R$ 0,50 em vez de R$ 0,70, podemos forçar que 4 cópias custem R$ 2,10 + R$ 0,50 = R$ 2,60. R$ 2,60 é R$ 2,00 + R$ 0,60. Logo, em vez de usarmos a função de preço $f(x) = 0.5x$ para $x$ entre 4 e 10, podemos usar a função $f(x) = 0.5x + 0.6$.

Se repetirmos o mesmo raciocínio para as outras interseções, a tabela de preços final fica assim:

(Isso aqui é só um exercício. Por favor, não façam isso, donos de gráficas!)

Agora note que as coisas passam a fazer mais sentido (embora muito mais caras):

• 3 cópias custam R$ 2,10 e 4 cópias custam R$ 2,60;
• 10 cópias custam R$ 5,60 e 11 cópias custam R$ 6,00;
• 20 cópias custam R$ 9,60 e 21 cópias custam R$ 9,90;
• 50 cópias custam R$ 18,60 e 51 cópias custam R$ 18,85;
• 100 cópias custam R$ 31,10 e 101 cópias custam R$ 31,30.

O gráfico monótono (e bonito) comprova:

Baseando-me no programa KBruch (um joguinho educativo do KDE que serve pra somar e subtrair duas frações) resolvi fazer uma função que calculasse MMC (pra dar o resultado do KBruch bem rápido! Hehehe). A função recebe dois argumentos: o número de termos e os termos (num vetor) e ficou bem simpes (e eu até comentei). Vejam:

//Função para calcular o MMC

#include <stdio.h>

int mmc(int *num, int ntermos) {
	int i, maior=0, a, j, c;

	//Descobrindo o maior número
	for (i=0; i<ntermos; i++) {
		if (num[i]>maior) {
			maior=num[i];
		}
	}

	for (i=1; c!=1; i++) {
		c=1;
		a=maior*i;
		//Verificando se o maior número vezes o i atual é divisível por todos números do conjunto
		for (j=0; j<ntermos; j++) {
			if (a%num[j]) {
				c=0;
			}
		}
	}

	return maior*(i-1); //Retornando resultado
}

int main() {
	int n[1001], nt, i;

	//Recebe número de termos
	printf("Quantos termos? ");
	scanf("%d", &nt);

	//Recebe números
	for (i=0; i<nt; i++) {
		printf("%d: ", i+1);
		scanf("%d", &n[i]);
	}

	//Chama a função e imprime o resultado
	printf("\nResultado: %d\n", mmc(n, nt));

	return 0;
}

Depois eu fiquei pensando que eu não estou calculando MMC como as pessoas calculam, então depois vou desenvolver uma outra função que calcule o MMC como as pessoas geralmente fazem, tipo assim:

[update] Já criei esse programa agora:

//MMC do jeito que as pessoas tiram geralmente

#include <stdio.h>
int res[10000], co=0;

int mmc(int *n, int nt) {
	int i, k, dv, at;

	for (i=0; i<nt-1; i++) {
		printf("%d, ", n[i]);
	}
	printf("%d | ", n[nt-1]);

	dv=0;
	for (i=2; !dv&&at!=nt; i++) {
		dv=0;
		at=0;
		for (k=0; k<nt; k++) {
			if (!(n[k]%i)) {
				dv=1;
				n[k]/=i;
			} else if (n[k]==1) {
				at+=1;
			}
		}
		if (dv) {
			printf("%d\n", i);
			res[co++]=i--;
		}
	}

	if (at==nt) {
		return 1;
	} else {
		return i*mmc(n, nt);
	}
}

int main(void) {
	int n[1001], nt, i, resultado;

	printf("MMC - Mínimo Múltiplo Comum\n");
	printf("http://tableless.tiagomadeira.net/script/mmc-comum.c\n\n");

	printf("Este programa calcula o MMC de vários termos inteiros que você especifica.\n");
	printf("Foi criado por Tiago Madeira usando um algoritmo semelhante ao que os professores\n");
	printf("de matemática ensinam nas escolas.\n\n");

	printf("De quantos números você quer calcular o MMC? ");
	scanf("%d", &nt);
	for (i=0; i<nt; i++) {
		printf("Digite o %d. número: ", i+1);
		scanf("%d", &n[i]);
	}
	printf("\n");

	printf("Para você calcular o MMC de vários termos, basta você ir dividindo eles por primos\n");
	printf("até todos se tornarem o número 1 (um). O programa faz isto exatamente como você\n");
	printf("faria. Acompanhe o cálculo abaixo:\n\n");

	resultado=mmc(n, nt);
	printf("X\n\n", resultado);
	for (i=0; i<co-1; i++) {
		printf("%d . ", res[i]);
	}
	printf("%d = %d\n", res[co-1], resultado);

	printf("Ou seja, o menor número que é divisível por todos os números que você colocou é\n");
	printf("este. Isto tem grandes utilidades e uma delas (talvez a mais utilizada) é fazer\n");
	printf("cálculos com frações de denominadores diferentes.\n\n");

	printf("Observação: Este cálculo é a maneira com que as pessoas costumam aprender, mas\n");
	printf("desenvolvi um outro programa que (além de falar menos) tem um custo menor\n");
	printf("(calcula de forma mais rápida). Ele está disponível em\n");
	printf("http://tableless.tiagomadeira.net/script/mmc.c\n");

	return 0;
}

[/update]

Mas meu programa faz assim:

Mas com dois termos é bem simples (tem uma função para dois termos no programa do KBruch). O legal é que a minha função funciona com o número de termos que eu quiser. Vou demonstrar como ela funciona para três termos.

Acho que fica mais simples de entender no método convencional mesmo…

E por causa disso, desenvolvi um programa que calcula da forma tradicional o MMC. É uma função recursiva. Ele é bem didático e mostra todo o raciocínio e algumas observações, porém o seu custo é maior (é mais demorado) que o primeiro.

Bom, nas aulas de matemática, andei desenvolvendo uns scripts muito úteis pra não precisar ficar calculando muito. Fiz um que calcula juros compostos, mas não publiquei. O que eu publiquei foi o que você digita o rótulo e o valor de cada pedaço de um gráfico de setores e ele devolve o número de graus que cada um deve ter (é uma simples regra de três, mas mesmo assim fiz pra brincar mesmo). Veja:

//Gerador de Gráficos em Setores
#include <stdio.h>
#define NMAX 1001

int main() {
	int n, i;
	float valor[NMAX], vt;
	char rotulo[NMAX][50];

	printf("Qual o número de valores? ");
	scanf("%d", &n);

	vt=0;
	for (i=1; i<=n; i++) {
		printf("Rótulo (%2d): ", i);
		scanf("%s", rotulo[i]);
		printf("Valor  (%2d): ", i);
		scanf("%f", &valor[i]);
		vt+=valor[i];
	}

	printf("\nResultados:\n(graus que devem ser usados na confecção do gráfico)\n");
	for (i=1; i<=n; i++) {
		printf("%s: %.2f graus\n", rotulo[i], valor[i]*360/vt);
	}
}

Hmmm… Tirei um 5,8 em biologia numa prova sobre biomas (minha menor nota em três anos) :blink: e errei uma questão numa prova de física, justamente aquilo que eu tinha feito um programa, a força gravitacional. Eu esqueci de elevar a notação científica da distância ao quadrado e com isto, meu resultado na prova foi 1,27 . 10^22 ao invés de 1,27 . 10^32. Mas tudo bem…