Vou neste e nos próximos artigos falar-lhes sobre a Teoria dos Grafos. É uma coisa que poderia ser complicada, então pra facilitar o entendimento eu resolvi que trabalharemos sempre com exemplos da “vida real”. Neste artigo, vamos trabalhar com o Orkut como base, partindo do princípio que todo mundo sabe o que é o Orkut.

Neste primeiro artigo, só falarei sobre a definição do grafo e sua utilidade. Apresentarei as definições de: vértice, aresta, grau, grafo orientado, grau de entrada e grau de saída. Então, vamos lá!

A definição de grafo é muito simples. Segundo o Professor Cid Carvalho de Souza: Uma forma de representar uma relação binária entre elementos de um conjunto. Bom… É simplesmente uma representação de relações (que chamamos de arestas) entre objetos, que chamamos de vértices. Vamos logo ao exemplo: a amizade no Orkut.

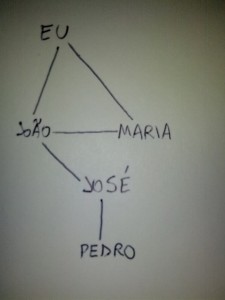
Estão vendo esta árvore? Esta é a representação que chamamos de grafo. Vamos supor que este é o grafo das amizades do Orkut e as bolinhas nele são as seguintes pessoas:

1. Eu
2. João
3. Maria
4. José
5. Pedro

Eu (número 1) tenho dois amigos: o João (número 2) e a Maria (número 3), porque estou ligado a eles. O João (número 2) tem três amigos: eu (número 1), a Maria (número 3) e o José (número 4). E assim podemos fazer com os outros contando as linhas que saem de cada pessoa.

Cada pessoa é um vértice e cada linha (relação entre duas pessoas) é uma aresta. Dizemos que é uma relação binária lá em cima, porque a relação é sempre entre dois vértices.

Os números de amigos que cada pessoa tem (o número de relações que cada vértice tem) é o que chamamos de “grau” de um vértice. Grau dos vértices do exemplo acima:

1. 2
2. 3
3. 2
4. 2
5. 1

Pra quê serve o grafo?

Ora, se você consegue contar as arestas que saem de cada vértice na programação (se você sabe fazer algo básico como calcular o grau de um vértice), você pode oferecer seus serviços ao Google e ganhar milhões, pois, como todos sabem, o Orkut não sabe fazer isso direito!

Brincadeiras a parte… Grafos são extremamente úteis porque são representações bastante simples (você teve dificuldade para entender minha árvore ali em cima?) e essa estrutura deles aparece em muitos problemas computacionais. Além disso, existem muitos algoritmos eficientes para problemas complexos que utilizam estas representações.

Definições até agora

Traduzindo os conceitos do Orkut para os grafos:

• Vértice: Pessoa.
• Aresta: Amizade entre uma pessoa e outra.
• Grau de um vértice: Número de amigos de uma pessoa.

Grafos Orientados

Um grafo é orientado quando eu sou seu amigo, mas você não é meu amigo. Você sabe que um grafo é orientado através da representação quando ele tem “setinhas”, como o grafo abaixo.

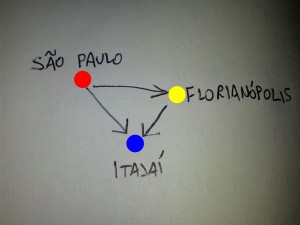
Vamos supor que isso aí é um mapa do Brasil. Ele despreza as cidades que não são importantes para o país, levando apenas em consideração portanto: São Paulo, Florianópolis e Itajaí.

• São Paulo é a bolinha vermelha.
• Florianópolis é a bolinha amarela.
• Itajaí é a bolinha azul.

As arestas indicam que há uma estrada para você ir de uma cidade para a outra, mas só dá pra ir no sentido da estrada, que as setas representam. Portanto, você pode ir de São Paulo a Florianópolis, de São Paulo a Itajaí e Florianópolis a Itajaí, mas não de Itajaí para qualquer outro lugar.

Grau dos Vértices

Os graus dos vértices neste segundo grafo seriam os seguintes, certo?

• São Paulo: 2
• Florianópolis: 2
• Itajaí: 2

Quase… Porém, nos grafos orientados nós temos dois tipos de grau diferentes. Dizemos que:

• grau de entrada é o número de arestas que apontam para o vértice; e
• grau de saída é o número de arestas que saem do vértice.

Portanto, os graus de entrada do nosso grafo são:

• São Paulo: 0
• Florianópolis: 1
• Itajaí: 2

E os graus de saída:

• São Paulo: 2
• Florianópolis: 1
• Itajaí: 0

Onde mais posso utilizar grafos?

Existem vários casos onde você vai querer usar grafos:

• Mapas
• Sua árvore genealógica
• Hierarquia de uma empresa
• Sistema de amizades do seu sistema de comunidades virtuais
• … e muito mais. Na OBI já apareceu até um jogo de dominó como problema de grafos!

Como veremos nos próximos artigos, tem algoritmo pra fazer “tudo” em grafos… Então representar alguma coisa em grafos é muito útil pra poder descobrir uma série de coisas.

A maioria das páginas que eu conheço sobre grafos são muito malignas porque apresentam uns 50 conceitos diferentes de grafos juntos (ex.: grafo conexo, grafo desconexo, caminho, ciclo, etc.). Nos meus artigos, devo tratar um assunto de cada vez para facilitar o entendimento. Então, vou parar por aqui hoje.

No próximo artigo: Como representar um grafo na programação? Você já pode ir pensando nisso…

No primeiro artigo desta série, expliquei o que é um algoritmo e até citei exemplos do cotidiano, como acordar ou falar com outra pessoa. Talvez você nem tenha se dado conta, mas usando listas numeradas eu representei os algoritmos ali presentes, inclusive destacando a entrada e a saída de cada situação-problema. Porém, não é sempre assim que representamos algoritmos.

Não existe uma regra padrão para a representação de algoritmos. Cada pessoa escreve de forma diferente, mas o importante é ser legível e convencionado. Por exemplo, o livro Algoritmos: Teoria e Prática* traz nas páginas 14 e 15 convenções do pseudocódigo que utiliza no livro inteiro. Já eu, quando vou passar o mesmo algoritmo, utilizaria outro tipo de código, você pode utilizar outro, e por aí vai. Mas todos têm que ter o mesmo foco: legibilidade e fácil implementação para qualquer linguagem.

* A partir deste artigo, sempre que eu falar “Cormen”, “CLRS”, “Introduction to Algorithms” ou “Algoritmos: Teoria e Prática” estarei me referindo a um livro que é referência essencial nessa área. A versão que tenho (de onde tiro o número das páginas) é a tradução da segunda edição americana publicada pela Elsevier em 2002.

Os pseudocódigos costumam parecer um código em linguagem Pascal traduzido para a sua língua. :) Usam quase sempre estruturas que estamos acostumados a usar na programação, como se, enquanto, para, arrays, etc. Eles existem para que o algoritmo seja de fácil leitura para qualquer programador, que programe em qualquer linguagem “normal”. Veja o pseudocódigo do Insertion Sort, um algoritmo de ordenação de vetores bastante simples:

para j $\leftarrow{}$ 2 até comprimento do vetor, faça
 elemento $\leftarrow{}$ vetor[j]
 i $\leftarrow{}$ j - 1
 enquanto i > 0 e vetor[i] > elemento, faça
  vetor[i + 1] $\leftarrow{}$ vetor[i]
  i $\leftarrow{}$ i - 1
 fim-enquanto
 vetor[i + 1] $\leftarrow{}$ elemento
fim-para

(Não se preocupe em entender o que ele faz, AINDA, pois veremos isso mais adiante)

Se você programa em qualquer linguagem, você não terá dificuldade em traduzir esse pseudocódigo para ela. O pseudocódigo é sempre uma maneira bem simples de escrever o código. Veja por exemplo, o mesmo código em C:

for (j=2; vetor[j]!=NULL; j++) {
    elemento = vetor[j];
    for (i = j-1; i > 0 && vetor[i] > elemento; i--) {
        vetor[i+1] = vetor[i];
    }
    vetor[i+1] = elemento;
}

Você deve ter percebido que ao invés de usar três linhas com uma declaração, um condicional e um incremento, eu juntei todos num só for. Mas por isso o algoritmo é bem simples e sempre parte do princípio de que a sua linguagem é simples. Veja só a implementação do código em Pascal e compare-a com a do pseudocódigo:

for j:=2 to comprimento, do begin
    elemento := vetor[j];
    i := j-1;
    while i>0 && vetor[i] > elemento, do begin
        vetor[i+1] := vetor[i];
        i := i-1;
    end;
    vetor[i] := elemento;
end;

Linha por linha ela é exatamente igual! A única diferença é que o pseudocódigo é traduzido… Geralmente os pseudocódigos são parecidos sempre com essa base e suas implementações não são muito diferentes. E vai ser sempre dessa maneira que eu vou representar os algoritmos (usando pseudocódigos e alguns traduzindo para C para mostrar implementações). No entanto, qualquer dúvida sobre essa representação, fique a vontade para perguntar através dos comentários.

Um algoritmo é um procedimento computacional definido que recebe um ou mais valores (entrada) e produz um ou mais valores (saída). O algoritmo é aquela fórmula matemática, aquele pedaço de código, que fica ali no meio da entrada e da saída para transformar o primeiro no segundo.

Vamos supôr por exemplo que temos a função:

A sua entrada é o x e a sua saída é o y (ou f(x), o valor que a função retorna).

O algoritmo aqui seria o seginte:

1. Entrada: Receber o valor X.
2. Elevar X ao quadrado e guardar o número resultante como Z.
3. Dividir Z por 3 e guardar o número resultante como Y.
4. Saída: Imprimir o valor Y.

O algoritmo, portanto, é a lógica do nosso problema matemático, ou, informático. É a seqüência de passos que eu faço na minha cabeça (ou, quando é complexo, no papel) antes de escrever, em C, a função f:

int f(int x) {
   int z, y;
   z = pow(x, 2);
   y = z/3;
   return y;
}

Se formos pensar, veremos que tudo o que fazemos é um algoritmo, é um procedimento que recebe uma entrada e envia uma saída. Não só no computador, mas na vida. Quando eu falo com alguém, eu espero sua entrada (o que a pessoa fala pra mim), então penso e transformo essa entrada numa saída (a resposta que vou dar pra pessoa). E assim é com várias outras coisas. Podemos dizer também que acordar é um algoritmo, por exemplo:

1. Entrada: Meu cérebro disse que eu estou acordado!
2. Percebi que acordei, mas estou com sono. Espero um pouco.
3. Saída: Abrir os olhos.
4. Saída: Se espreguiçar.
5. Saída: Tirar a coberta.
6. Saída: Sentar na cama.
7. Saída: Sair da cama.

Podem existir vários algoritmos diferentes para resolver o mesmo problema. No caso de Acordar, cada um acorda de forma diferente, por exemplo. Foi até um exemplo meio estranho esse aí, mas outro algoritmo poderia dar outra saída, como por exemplo simplesmente abrir os olhos e cair da cama. Ou no caso acima da função matemática, poderíamos ter um algoritmo que fizesse a mesma coisa de maneira diferente também.

O algoritmo que usamos depende principalmente do tempo que ele demora pra ser executado e a memória que ele gasta no computador. Chamamos isso de custo. Quando começarmos a ver os algoritmos de ordenação de vetores (arrays), veremos que cada algoritmo faz uma coisa diferente, mas todos servem para o mesmo propósito: ordenar o vetor. Para uma entrada pequena, um pode ser mais rápido… Para uma maior, outro. Portanto, o algoritmo que queremos usar (o tempo que ele vai demorar pra ser executado e a memória que ele vai gastar no computador) depende principalmente do tamanho da entrada (que chamamos de n e no exemplo da função seria lá em cima seria a variável x).

Na maioria dos casos (e vai ser sempre assim aqui nos meus artigos), a entrada será o teclado (por exemplo, o usuário digita o X para a função) e a saída será a tela (por exemplo, o programa imprime o resultado da função, o Y, para a tela). Essas são a entrada e saída padrão (standard input output do C), que é usada nas olimpíadas e na maioria dos problemas que resolvemos no computador.

Em resumo, portanto, um algoritmo é a lógica de um programa computacional. Nos próximos artigos, isso deverá ser mais esclarecido e começaremos a ver algoritmos “de verdade” ;)

Qualquer dúvida, sugestão ou notificação de erro; poste um comentário ou me envie um e-mail (não só nesse, mas também nos próximos artigos). Espero que gostem.