No último artigo, conhecemos a representação chamada “grafo” da seguinte maneira:
Como todos sabemos, seria bem difícil trabalhar uma árvore assim na programação! Por isso, existem várias maneiras de representar um grafo. Nesta série só vou usar as duas mais populares:
- Matriz de Adjacência
- Lista de Adjacência
Poderíamos falar também sobre a Matriz de Incidência, mas eu nunca precisei utilizá-la, então prefiro só entrar nessas duas mesmo.
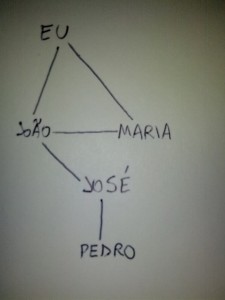
Cada vértice é um número
Para representar um grafo, cada vértice sempre vai ser um número. No caso de você querer representar amizade entre duas pessoas, como no exemplo do Orkut no último artigo, você cria um vetor chamado nome[] que contém o nome de cada número…
- Eu
- João
- Maria
- José
- Pedro
Matriz de Adjacência
A matriz de adjacência é uma matriz de N x N (onde N é o número de vértices do grafo). Ela inicialmente é preenchida toda com 0 e quando há uma relação entre o vértice do x (número da coluna) com o do y (número da linha), matriz[x][y] é marcado um 1.
Vamos escrever este grafo aqui usando uma matriz de adjacência:
Matriz Inicial
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 |
Relações do nosso grafo
Já que o grafo não é orientado, a relação 1–2 significa 2–1 também.
- 1–2 (2–1)
- 1–3 (3–1)
- 2–3 (3–2)
- 2–4 (4–2)
- 4–5 (5–4)
Essas são as cinco arestas do nosso grafo. Vamos representá-la na matriz de adjacência:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 1 | 1 | |||
| 2 | 1 | 1 | 1 | ||
| 3 | 1 | 1 | |||
| 4 | 1 | 1 | |||
| 5 | 1 |
Simetria
Uma das características da matriz de adjacência quando o grafo não é orientado é a simetria encontrada na “diagonal”. É interessante que se lermos uma coluna de índice v ou uma linha de índice v vamos encontrar a mesma coisa.
Problemas da OBI
Alguns desses programas são complicados, mas isto não entra em questão. Apenas dê uma olhada no recebimento da entrada deles. Todos estão em C. O que eles têm em comum é a utilização de uma matriz de adjacência para guardar o grafo (geralmente nomeada g):
- Ambulância
- Batuíra +
- Carga Pesada * +
- Dengue
- Dominó
- Manutenção
- Número de Erdos X
- Orkut *
- Pedágio
- Rede Ótica
* – Grafo orientado
+ – Grafo ponderado (veremos no próximo artigo)
X – Não queira ver esse problema. Nunca vi solução mais feia. Já estou providenciando uma implementação mais decente… ;)
Descobrir o grau de cada vértice
Eu não disse pra vocês que era fácil conseguir emprego no Orkut? Hehehe… Vamos pensar como podemos descobrir o grau (relembrando… o número de arestas que cada vértice tem OU o número de amigos que cada pessoa tem) na matriz de adjacências. Não basta contar quantos 1s tem na sua linha correspondente? Então façamos isto.
para i 1 até N, faça
grau 0
para j 1 até N, faça
se matriz[i][j] = 1, então
grau grau + 1
fim-se
fim-para
imprima “O vértice ” i ” tem grau ” grau ”.”
fim-para
O custo é até no melhor caso… Será que não há uma maneira mais simples de fazer isso? Imagina um negócio do tamanho do Orkut. Milhões de pessoas… Não seria bem mais fácil se ao invés de termos que passar por todos os vértices, só passarmos pelos amigos? Não poderíamos colocar somente seus amigos num vetor? É por isto que utilizamos a lista de adjacência.
Lista de Adjacência
A lista de adjacência consiste em criar um vetor para cada vértice. Este vetor contém cada vértice que o vértice “conhece” (tem uma aresta para). Geralmente é representada com uma matriz, porque cada vértice vai precisar de um vetor diferente, não é? Já que eu não vou ser duas vezes “amigo” de ninguém, então podemos fazer uma matriz de NxN.
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 |
A lista consiste em escrever para cada número de linha (= vértice) seus amigos, da seguinte maneira:
- 2, 3
- 1, 3, 4
- 1, 2
- 2, 5
- 4
Portanto, na programação seria representado da seguinte maneira:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| 2 | 1 | 3 | 4 | ||
| 3 | 1 | 2 | |||
| 4 | 2 | 5 | |||
| 5 | 4 |
O método da lista de adjacências tem várias vantagens: dependendo de como você implementa você não precisa inicializar a lista (zerar), as buscas são bem mais rápidas (você só passa pelos vértices que são “amigos” do atual) e geralmente você já tem o grau do vértice na ponta da língua (eu, pelo menos, sempre uso um vetor cont que contém o número de amigos de cada vértice para ficar mais fácil inserir o próximo elemento na lista – lista[cont[v]++]=w).
Como implementar
Vamos trabalhar com uma entrada de vários x, y, indicando relação entre x-y (y-x) até que x=0 e y=0. O grafo não é orientado.
Matriz de Adjacências
para i 1 até N, faça
para j 1 até N, faça
matriz[i][j] 0
fim-para
fim-para
enquanto (recebe x, y e x 0), faça
matriz[x][y] 1
matriz[y][x] 1
fim-enquanto
Tem vários exemplos implementados em C [aqui][14].
Lista de Adjacências
para i 1 até N, faça
grau[i] 0
fim-para
enquanto (recebe x, y e x 0), faça
lista[x]grau[x]++] y
lista[y]grau[y]++] x
fim-enquanto
Para quem não programa em C, o variavel++ significa “incrementar variavel depois da instrução atual”.
As duas juntas
para i 1 até N, faça
para j 1 até N, faça
matriz[i][j] 0
fim-para
grau[i] 0
fim-para
enquanto (recebe x, y e x 0), faça
matriz[x][y] 1
matriz[y][x] 1
lista[x]grau[x]++] y
lista[y]grau[y]++] x
fim-enquanto
Qual a representação que devo utilizar?
Isso depende totalmente do problema. Em alguns casos, o mais barato é usar as duas representações juntas. As vantagens da lista de adjacências eu já escrevi [aqui][15]. A única vantagem da matriz de adjacências é você em tempo constante (não é nem linear) saber se um vértice é amigo de outro. Afinal, basta testar matriz[v][w].
Até maio do ano passado, eu não tinha aprendido isso direito e sempre usava a matriz de adjacências. Por isso muitos dos meus problemas estão resolvidos de forma pouco eficiente… e isso pode ser crucial numa prova. Por isso, saiba usar as duas formas!