Um grafo é ponderado quando suas arestas possuem um peso. O que significa isso? Bom… Vamos supor que eu queira ir de um lugar pra outro, mas o mais importante pra mim não seja a distância entre eles mas o pedágio que vou ter que pagar para pegar cada aresta (estrada). Nesse caso, o peso de cada aresta seria o custo que eu tenho pra passar pela estrada. O problema então seria calcular o caminho onde eu pago menos (o caminho que tem a menor soma de preços) e não o menor caminho no grafo “não-ponderado” (onde consideramos aresta=1 e nada=0).

Neste grafo, por exemplo, o menor caminho de 0 a 3 não é a aresta 0–3, mas sim a aresta 0–2 e depois a aresta 2–3.

Para representar um grafo ponderado usando a matriz de adjacência, onde antes marcávamos “1”, marcamos o peso que temos de ir de um vértice para o outro e onde marcávamos “0” marcamos $\infty{}$ (infinito).

Na verdade, só fazemos isso do infinito porque neste caso iríamos querer o menor caminho e o 0 poderia atrapalhar, porque poderíamos ter um caminho sem pedágio, por exemplo, mas isso sempre depende do caso.

Usando listas de adjacência, podemos representar as ligações de cada vértice com dois vetores (um para dizer a qual ele se liga e outro o peso desta ligação) ou com um vetor de structs como:

struct edge {
  int destino, peso;
};

No último artigo, conhecemos a representação chamada “grafo” da seguinte maneira:

Como todos sabemos, seria bem difícil trabalhar uma árvore assim na programação! Por isso, existem várias maneiras de representar um grafo. Nesta série só vou usar as duas mais populares:

• Matriz de Adjacência
• Lista de Adjacência

Poderíamos falar também sobre a Matriz de Incidência, mas eu nunca precisei utilizá-la, então prefiro só entrar nessas duas mesmo.

Cada vértice é um número

Para representar um grafo, cada vértice sempre vai ser um número. No caso de você querer representar amizade entre duas pessoas, como no exemplo do Orkut no último artigo, você cria um vetor chamado nome[] que contém o nome de cada número…

1. Eu
2. João
3. Maria
4. José
5. Pedro

Matriz de Adjacência

A matriz de adjacência é uma matriz de N x N (onde N é o número de vértices do grafo). Ela inicialmente é preenchida toda com 0 e quando há uma relação entre o vértice do x (número da coluna) com o do y (número da linha), matriz[x][y] é marcado um 1.

Vamos escrever este grafo aqui usando uma matriz de adjacência:

Matriz Inicial

Relações do nosso grafo

Já que o grafo não é orientado, a relação 1–2 significa 2–1 também.

• 1–2 (2–1)
• 1–3 (3–1)
• 2–3 (3–2)
• 2–4 (4–2)
• 4–5 (5–4)

Essas são as cinco arestas do nosso grafo. Vamos representá-la na matriz de adjacência:

Simetria

Uma das características da matriz de adjacência quando o grafo não é orientado é a simetria encontrada na “diagonal”. É interessante que se lermos uma coluna de índice v ou uma linha de índice v vamos encontrar a mesma coisa.

Problemas da OBI

Alguns desses programas são complicados, mas isto não entra em questão. Apenas dê uma olhada no recebimento da entrada deles. Todos estão em C. O que eles têm em comum é a utilização de uma matriz de adjacência para guardar o grafo (geralmente nomeada g):

• Ambulância
• Batuíra +
• Carga Pesada * +
• Dengue
• Dominó
• Manutenção
• Número de Erdos X
• Orkut *
• Pedágio
• Rede Ótica

* – Grafo orientado
+ – Grafo ponderado (veremos no próximo artigo)
X – Não queira ver esse problema. Nunca vi solução mais feia. Já estou providenciando uma implementação mais decente… ;)

Descobrir o grau de cada vértice

Eu não disse pra vocês que era fácil conseguir emprego no Orkut? Hehehe… Vamos pensar como podemos descobrir o grau (relembrando… o número de arestas que cada vértice tem OU o número de amigos que cada pessoa tem) na matriz de adjacências. Não basta contar quantos 1s tem na sua linha correspondente? Então façamos isto.

para i $\leftarrow{}$ 1 até N, faça
 grau $\leftarrow{}$ 0
 para j $\leftarrow{}$ 1 até N, faça
  se matriz[i][j] = 1, então
   grau $\leftarrow{}$ grau + 1
  fim-se
 fim-para
 imprima “O vértice ” i ” tem grau ” grau ”.”
fim-para

O custo é $\Theta{}(n^{2})$ até no melhor caso… Será que não há uma maneira mais simples de fazer isso? Imagina um negócio do tamanho do Orkut. Milhões de pessoas… Não seria bem mais fácil se ao invés de termos que passar por todos os vértices, só passarmos pelos amigos? Não poderíamos colocar somente seus amigos num vetor? É por isto que utilizamos a lista de adjacência.

Lista de Adjacência

A lista de adjacência consiste em criar um vetor para cada vértice. Este vetor contém cada vértice que o vértice “conhece” (tem uma aresta para). Geralmente é representada com uma matriz, porque cada vértice vai precisar de um vetor diferente, não é? Já que eu não vou ser duas vezes “amigo” de ninguém, então podemos fazer uma matriz de NxN.

A lista consiste em escrever para cada número de linha (= vértice) seus amigos, da seguinte maneira:

1. 2, 3
2. 1, 3, 4
3. 1, 2
4. 2, 5
5. 4

Portanto, na programação seria representado da seguinte maneira:

O método da lista de adjacências tem várias vantagens: dependendo de como você implementa você não precisa inicializar a lista (zerar), as buscas são bem mais rápidas (você só passa pelos vértices que são “amigos” do atual) e geralmente você já tem o grau do vértice na ponta da língua (eu, pelo menos, sempre uso um vetor cont que contém o número de amigos de cada vértice para ficar mais fácil inserir o próximo elemento na lista – lista[cont[v]++]=w).

Como implementar

Vamos trabalhar com uma entrada de vários x, y, indicando relação entre x-y (y-x) até que x=0 e y=0. O grafo não é orientado.

Matriz de Adjacências

para i $\leftarrow{}$ 1 até N, faça
 para j $\leftarrow{}$ 1 até N, faça
  matriz[i][j] $\leftarrow{}$ 0
 fim-para
fim-para

enquanto (recebe x, y e x $\neq{}$ 0), faça
 matriz[x][y] $\leftarrow{}$ 1
 matriz[y][x] $\leftarrow{}$ 1
fim-enquanto

Tem vários exemplos implementados em C [aqui][14].

Lista de Adjacências

para i $\leftarrow{}$ 1 até N, faça
 grau[i] $\leftarrow{}$ 0
fim-para

enquanto (recebe x, y e x $\neq{}$ 0), faça
 lista[x]grau[x]++] $\leftarrow{}$ y
 lista[y]grau[y]++] $\leftarrow{}$ x
fim-enquanto

Para quem não programa em C, o variavel++ significa “incrementar variavel depois da instrução atual”.

As duas juntas

para i $\leftarrow{}$ 1 até N, faça
 para j $\leftarrow{}$ 1 até N, faça
  matriz[i][j] $\leftarrow{}$ 0
 fim-para
 grau[i] $\leftarrow{}$ 0
fim-para

enquanto (recebe x, y e x $\neq{}$ 0), faça
 matriz[x][y] $\leftarrow{}$ 1
 matriz[y][x] $\leftarrow{}$ 1
 lista[x]grau[x]++] $\leftarrow{}$ y
 lista[y]grau[y]++] $\leftarrow{}$ x
fim-enquanto

Qual a representação que devo utilizar?

Isso depende totalmente do problema. Em alguns casos, o mais barato é usar as duas representações juntas. As vantagens da lista de adjacências eu já escrevi [aqui][15]. A única vantagem da matriz de adjacências é você em tempo constante (não é nem linear) saber se um vértice é amigo de outro. Afinal, basta testar matriz[v][w].

Até maio do ano passado, eu não tinha aprendido isso direito e sempre usava a matriz de adjacências. Por isso muitos dos meus problemas estão resolvidos de forma pouco eficiente… e isso pode ser crucial numa prova. Por isso, saiba usar as duas formas!

Resolvi fazer uma pausa nos algoritmos de ordenação para mostrar como podemos usar os conhecimentos já adquiridos de maneira prática. Vamos neste artigo resolver o problema Mini-Poker, que caiu na prova da Programação Nível 2 (categoria para pessoas até 19 anos ou primeiro ano da faculdade) da Olimpíada Brasileira de Informática de 2005.

Esse post ficou gigante, mas é muito simples. Leia com atenção e acho que você não terá problemas… ;)

Objetivos

Com esta resolução de problema, espero treinar com vocês o conceito de:

• Interpretação do Probema
• Entrada e Saída
• Ordenação por Inserção
• Pseudocódigo

Acho que será legal para pôrmos em prática o que já estudamos sobre algoritmos.

O problema é bem simples, mas é só pra iniciar.

Enunciado

Mini-Poker é o nome do jogo de cartas que é uma simplificação de Poker, um dos mais famosos jogos de cartas do mundo. Mini-Poker é jogado com um baralho normal de 52 cartas, com quatro naipes (copas, paus, espadas e ouro), cada naipe compreendendo treze cartas (Ás, 2, 3, 4, 5, 6, 7, 8, 9, 10, Valete, Dama, Rei).

No início do jogo, cada jogador recebe cinco cartas. O conjunto de cinco cartas vale um certo número de pontos, de acordo com as regras descritas abaixo. Diferentemente do jogo de Poker normal, em Mini-poker o naipe das cartas é desconsiderado. Assim, para simplificar a descrição do jogo, vamos utilizar os números de 1 a 13 para identificar as cartas do baralho, na ordem dada acima. Uma outra diferença é que pode ocorrer empate entre mais de um vencedor; nesse caso os vencedores dividem o prêmio.

As regras para pontuação em Mini-Poker são as seguintes:

1. Se as cinco cartas estão em seqüência a partir da carta $x$ (ou seja, os valores das cartas são $x$, $x+1$, $x+2$, $x+3$ e $x+4$), a pontuação é $x+200$ pontos. Por exemplo, se as cartas recebidas são 10, 9, 8, 11 e 12, a pontuação é 208 pontos.
2. Se há quatro cartas iguais $x$ (uma quadra, ou seja, os valores das cartas são $x$, $x$, $x$, $x$ e $y$), a pontuação é $x+180$ pontos. Por exemplo, se as cartas recebidas são 1, 1, 1, 10 e 1, a pontuação é 181 pontos.
3. Se há três cartas iguais $x$ e outras duas cartas iguais $y$ (uma trinca e um par, ou seja, os valores das cartas são $x$, $x$, $x$, $y$ e $y$), a pontuação é $x+160$ pontos. Por exemplo, se as cartas recebidas são 10, 4, 4, 10 e 4, a pontuação é 164 pontos.
4. Se há três cartas iguais $x$ e duas outras cartas diferentes $y$ e $z$ (uma trinca, ou seja, os valores das cartas são $x$, $x$, $x$, $y$ e $z$), a pontuação é $x+140$ pontos. Por exemplo, se as cartas recebidas são 2, 3, 2, 2 e 13, a pontuação é 142 pontos.
5. Se há duas cartas iguais $x$, duas outras cartas iguais $y$ ($x \neq{} y$) e uma outra carta distinta $z$ (dois pares, ou seja, os valores das cartas são $x$, $x$, $y$, $y$ e $z$), a pontuação é $3 \times{} x + 2 \times{} y + 20$ pontos, em que $x > y$. Por exemplo, se as cartas recebidas são 12, 7, 12, 8 e 7, a pontuação é 70 pontos.
6. Se há apenas duas cartas iguais $x$ e as outras são distintas (um par, ou seja, os valores das cartas são $x$, $x$, $y$, $z$ e $t$), a pontuação é $x$ pontos. Por exemplo, se as cartas recebidas são 12, 13, 5, 8 e 13, a pontuação é 13 pontos.
7. Se todas as cartas são distintas, não há pontuação.

Tarefa

Escreva um programa que, fornecidas as cartas dadas a um jogador, calcule a pontuação do jogador naquela jogada.

Entrada

A entrada é composta por vários casos de teste, cada um correspondendo a uma jogada. A primeira linha da entrada contém um número inteiro $N$ que indica o número de casos de teste ($1 \leq{} N \leq{} 100$). Cada uma das $N$ linhas seguintes contém cinco números inteiros $C\_{1}$, $C\_{2}$, $C\_{3}$, $C\_{4}$ e $C\_{5}$, representando as cinco cartas recebidas por um jogador ($1 \leq{} C\_{1}, C\_{2}, C\_{3}, C\_{4}, C\_{5} \leq{} 13$).

A entrada deve ser lida do dispositivo de entrada padrão (normalmente o teclado).

Saída

Para cada caso de teste da entrada, seu programa deve produzir três linhas na saída. A primeira linha deve conter um identificador do caso de teste, no formato “Teste n”, onde n é numerado seqüencialmente a partir de 1. A segunda linha deve conter a pontuação do jogador considerando as cinco cartas recebidas. A terceira linha deve ser deixada em branco. A grafia mostrada no Exemplo de Saída, abaixo, deve ser seguida rigorosamente.

A saída deve ser escrita no dispositivo de saída padrã (normalmente a tela).

Restrições

$1 \leq{} N \leq{} 100$ $1 \leq{} C\_{1}, C\_{2}, C\_{3}, C\_{4}, C\_{5} \leq{} 13$

Exemplo de Entrada

2
12 3 10 3 12
1 2 3 5 4

Saída para o Exemplo de Entrada

Teste 1
62

Teste 2
201

Comentários sobre os problemas de olimpíadas

Todos os problemas passados em competições de programação tem um enunciado parecido com o desse. São especificados todos os limites (restrições), é dito exatamente como será a entrada e como deve ser a saída e geralmente tem uma historinha no começo… :D

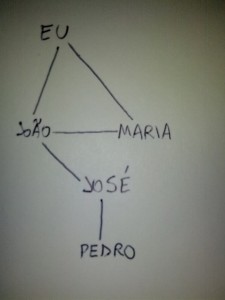
Bom… Todos esses dados são fundamentais. Alguns limites nem vamos usar, não tem importância para a nossa solução, mas pode ter importância para outra pessoa que queira implementar um algoritmo diferente. A sintaxe da entrada e da saída são extremamente importantes. Na prova da Seletiva IOI do ano passado, eu quase perdi 60 pontos (6 casos de teste) na solução de um problema simples porque meu programa desprezava um espaço no início de uma frase quando imprimia uma saída. E mesmo a historinha do começo é fundamental. Ela sempre dá boas dicas e algumas vezes até ilustra o problema (às vezes a gente nem lê o enunciado e já sabe que é um problema de grafos!)

Mas vamos a solução deste problema…

Por onde começar?

Com o tempo você pode decidir fazer um caminho diferente, mas eu sugiro começar sempre pelo recebimento da entrada. Aliás, acho que isto é atípico, porque a maioria das pessoas prefere ler bastante o problema e desenvolver todo o algoritmo a mão antes de botar a mão na massa. Eu acho que depois que a gente recebe a entrada, fica bem mais fácil fazer o resto e a gente pode ir pensando enquanto a gente recebe a entrada! Então, depois que lemos o problema e já entendemos tudo o que ele quer, vamos fazer a entrada!

O problema fala que começa nos dando um número N que será o número de casos de teste que teremos que receber depois. Sem dificuldade podemos escrever o _pseudo_código a seguir:

recebe N
para nteste $\leftarrow{}$ 1 até N, faça
fim-para

Já chamo a variável que loopa como nteste, porque já li a saída do problema e sei que vou precisar imprimir o número de caad caso de teste… ;)

Aí o enunciado diz que Cada uma das $N$ linhas seguintes contém cinco números inteiros $C\_{1}$, $C\_{2}$, $C\_{3}$, $C\_{4}$ e $C\_{5}$, representando as cinco cartas recebidas por um jogador ($1 \leq{} C\_{1}, C\_{2}, C\_{3}, C\_{4}, C\_{5} \leq{} 13$). Então, vamos receber os cinco números em cada iteração e colocá-los num vetor, é claro!

recebe N
para nteste $\leftarrow{}$ 1 até N, faça
 recebe $C_{1}, C_{2}, C_{3}, C_{4}, C_{5}$
fim-para

E a entrada está pronta.

Desenvolvimento

O programa se baseia em encontrarmos valores iguais nos elementos do vetor. O que podemos fazer para facilitar essa tarefa?

Isso mesmo: A ordenação! :D Se os elementos estiverem ordenados, ficará bem mais fácil para procurarmos quatro números iguais, porque eles não poderão ser qualquer uma das possibilidades, mas somente $C_{1}, C_{2}, C_{3}, C_{4}$ ou $C_{2}, C_{3}, C_{4}, C_{5}$.

Aí que algoritmos devemos implementar para ordenar? Isso é uma conclusão que vamos chegar no final de nossa série, mas para este algoritmo não tem solução melhor que a Ordenação por Inserção. É um caso pequeno (n=5) e a Ordenação por Inserção é mais rápida que a por Seleção, porque o seu melhor caso é uma função linear. Então, vamos implementar o Insertion Sort no nosso algoritmo:

recebe N
para nteste $\leftarrow{}$ 1 até N, faça
 recebe $C_{1}, C_{2}, C_{3}, C_{4}, C_{5}$
 // início da ordenação por inserção
 para j $\leftarrow{}$ 2 até 5
  elemento $\leftarrow{}$ $C_{j}$
  i $\leftarrow{}$ j-1
  enquanto i > 0 e $C_{i}$ > elemento, faça
   $C_{i+1}$ $\leftarrow{}$ $C_{i}$
   $i$ $\leftarrow{}$ $C_{i-1}$
  fim-enquanto
  $C_{i+1}$ $\leftarrow{}$ elemento
 fim-para
 // fim da ordenação por inserção
fim-para

O bom desses algoritmos de ordenação é que sua lógica é muito simples e por isso é fácil decorá-los… Ao menos o Insertion Sort e o Selection Sort são algoritmos básicos que todo programador deve conhecer bem. Bom… Acredito que vocês não tenham tido dificuldade pra entender até aqui. A cor vermelha no pseudocódigo eu vou usar daqui pra frente para um comentário, que aliás, é uma excelente prática de boa programação.

O resto do problema precisa calcular quantos pontos o cara fez, baseado em suas cartas, agora já ordenadas. Para isto vamos criar uma função para testar vários se e retornar o resultado.

Eu poderia tirar os se aninhados, mas assim fica mais fácil a compreensão.

Como vamos ver com os pseudocódigos a seguir, é fácil testar cada uma das regras com o vetor ordenado:

Primeira Regra – Seqüência

Se as cinco cartas estão em seqüência a partir da carta $x$(ou seja, os valores das cartas são $x$, $x+1$, $x+2$, $x+3$ e $x+4$), a pontuação é $x+200$ pontos. Por exemplo, se as cartas recebidas são 10, 9, 8, 11 e 12, a pontuação é 208 pontos.

se $C_{1} = C_{2}-1$ e $C_{2} = C_{3}-1$ e $C_{3}=C_{4}-1$ e $C_{4}=C_{5}-1$, então
 retorna $C_{1}+200$
fim-se

Segunda Regra – Quadra

Se há quatro cartas iguais $x$ (uma quadra, ou seja, os valores das cartas são $x$, $x$, $x$, $x$ e $y$), a pontuação é $x+180$ pontos. Por exemplo, se as cartas recebidas são 1, 1, 1, 10 e 1, a pontuação é 181 pontos.

se $C_{1} = C_{2} = C_{3} = C_{4}$ ou $C_{2} = C_{3} = C_{4} = C_{5}$, então
 retorna $C_{2}+180$
fim-se

Aqui retornamos $C\_{2}$ porque ele será sempre parte da quadra (ela começando em $C\_{1}$ ou $C\_{2}$).

Terceira e Quarta Regra – Trinca

Se há três cartas iguais $x$ e outras duas cartas iguais $y$ (uma trinca e um par, ou seja, os valores das cartas são $x$, $x$, $x$, $y$ e $y$), a pontuação é $x+160$ pontos. Por exemplo, se as cartas recebidas são 10, 4, 4, 10 e 4, a pontuação é 164 pontos.

se $C_{1} = C_{2} = C_{3}$ ou $C_{2} = C_{3} = C_{4}$ ou $C_{3} = C_{4} = C_{5}$, então
 se ( $C_{1} \neq{} C_{3}$ e $C_{1} = C_{2}$ ) ou ( $C_{3} \neq{} C_{5}$ e $C_{4} = C_{5}$ ), então
  retorna $C_{3}+160$

Se há três cartas iguais $x$ e duas outras cartas diferentes $y$ e $z$ (uma trinca, ou seja, os valores das cartas são $x$, $x$, $x$, $y$ e $z$), a pontuação é $x+140$ pontos. Por exemplo, se as cartas recebidas são 2, 3, 2, 2 e 13, a pontuação é 142 pontos.

 senão
  retorna $C_{3} + 140$
 fim-se
fim-se

Note que aqui retornamos $C\_{3}$ porque ele será sempre parte da trinca (o mesmo motivo que retornarmos $C\_{2}$ para a quadra).

Quinta Regra – Duas Duplas

Se há duas cartas iguais $x$, duas outras cartas iguais $y$ ($x \neq{} y$) e uma outra carta distinta $z$ (dois pares, ou seja, os valores das cartas são $x$, $x$, $y$, $y$ e $z$), a pontuação é $3 \times{} x + 2 \times{} y + 20$ pontos, em que $x > y$. Por exemplo, se as cartas recebidas são 12, 7, 12, 8 e 7, a pontuação é 70 pontos.

se $C_{1} = C_{2}$ ou $C_{2} = C_{3}$, então
 se $C_{3} = C_{4}$ ou $C_{4} = C_{5}$, então
  retorna $3 \times{} C_{4} + 2 \times{} C_{2} + 20$
 fim-se
fim-se

$C\_{2}$ será sempre elemento da menor dupla e $C\_{4}$ será sempre elemento da maior dupla. Por isso usamos eles como $y$ e $x$, respectivamente.

Sexta Regra – Dupla

Se há apenas duas cartas iguais $x$ e as outras são distintas (um par, ou seja, os valores das cartas são $x$, $x$, $y$, $z$ e $t$), a pontuação é $x$ pontos. Por exemplo, se as cartas recebidas são 12, 13, 5, 8 e 13, a pontuação é 13 pontos.

se $C_{1} = C_{2}$ ou $C_{2} = C_{3}$, então
 retorna $C_{2}$
senão se $C_{3} = C_{4}$ ou $C_{4} = C_{5}$, então
 retorna $C_{4}$
fim-se

Separei em dois SEs porque senão não saberíamos que valor retornar.

Sétima Regra

Se todas as cartas são distintas, não há pontuação.

retorna 0

Função Inteira

Juntando todos os SEs, temos:

função pontua (C)
 // primeira regra
 se $C_{1} = C_{2}-1$ e $C_{2} = C_{3}-1$ e $C_{3}=C_{4}-1$ e $C_{4}=C_{5}-1$, então
  retorna $C_{1}+200$
 fim-se
 
 // segunda regra
 se $C_{1} = C_{2} = C_{3} = C_{4}$ ou $C_{2} = C_{3} = C_{4} = C_{5}$, então
  retorna $C_{2}+180$
 fim-se
 
 //terceira e quarta regra
 se $C_{1} = C_{2} = C_{3}$ ou $C_{2} = C_{3} = C_{4}$ ou $C_{3} = C_{4} = C_{5}$, então
  se ( $C_{1} \neq{} C_{3}$ e $C_{1} = C_{2}$ ) ou ( $C_{3} \neq{} C_{5}$ e $C_{4} = C_{5}$ ), então
   retorna $C_{3}+160$
  senão
   retorna $C_{3} + 140$
  fim-se
 fim-se
 
 // quinta regra
 se $C_{1} = C_{2}$ ou $C_{2} = C_{3}$, então
  se $C_{3} = C_{4}$ ou $C_{4} = C_{5}$, então
   retorna $3 \times{} C_{4} + 2 \times{} C_{2} + 20$
  fim-se
 fim-se
 
 // sexta regra
 se $C_{1} = C_{2}$ ou $C_{2} = C_{3}$, então
  retorna $C_{2}$
 senão se $C_{3} = C_{4}$ ou $C_{4} = C_{5}$,
 então
  retorna $C_{4}$
 fim-se
 
 // sétima regra
 retorna 0
fim-função

Já que a função retorna assim que encontra um resultado, não há risco de ocorrer nada errado (por exemplo, uma quadra é sempre uma trinca, que é sempre uma dupla). Agora basta colocarmos esta função no nosso código e adaptar para a saída ser igual a que o problema pede.

Saída

Para chegar a saída, basta fazermos o programa imprimir Teste nteste e depois o retorno da função pontua. Com isto, temos:

recebe N
para nteste $\leftarrow{}$ 1 até N, faça
 recebe $C_{1}, C_{2}, C_{3}, C_{4}, C_{5}$
 // início da ordenação por inserção
 para j $\leftarrow{}$ 2 até 5
  elemento $\leftarrow{}$ $C_{j}$
  i $\leftarrow{}$ j-1
  enquanto i > 0 e $C_{i}$ > elemento, faça
   $C_{i+1}$ $\leftarrow{}$ $C_{i}$
   $i$ $\leftarrow{}$ $C_{i-1}$
  fim-enquanto
  $C_{i+1}$ $\leftarrow{}$ elemento
 fim-para
 // fim da ordenação por inserção

 imprime “Teste ”
 imprime linha testen
 imprime linha pontua(C)
 imprime linha
fim-para

Fiz essa saída assim pra se parecer com Pascal, mas para cada linguagem ela pode ser bem diferente… Vejamos dois exemplos…

C

printf("Teste %d\n%d\n\n", nteste, pontua(C));

PHP

echo "Teste ".$nteste."\n".pontua($C)."\n\n";

Comentários sobre o problema

Este problema é muito chato. É trivial, mas perdemos um tempo enorme escrevendo ses. Ninguém gosta de um problema como esse, mas quando cai numa olimpíada somos obrigados a resolver… hehehe… Mas, para a felicidade geral de todos, saibam que a maioria dos problemas de olimpíadas não são assim. Exigem mais lógica e menos código. Com o tempo, vamos pegando problemas mais difíceis. Espero só ter cumprido meu objetivo dando uma utilidade pra ordenação, entrada e saída e que vocês tenham entendido tudo.

Sugiro que quem esteja aprendendo algoritmos com meus artigos e já saiba programar um pouquinho, resolva alguns problemas simples do site da OBI, que separei especialmente pra vocês!

• Bits Trocados
• Calculando
• Cofrinhos da Vó Vitória
• Quermesse

E, gostaria de fixar, mais importante é a interpretação e o seu pensamento… Programar é fácil!

Hoje vou apresentar mais um algoritmo de ordenação de vetores. É a Ordenação por Seleção (ou Selection Sort). Sem mais papo e antes mesmo da explicação, vamos ao seu pseudocódigo:

para i $\leftarrow{}$ 1 até tamanho-1, faça
 minimo $\leftarrow{}$ i
 para j $\leftarrow{}$ i+1 até tamanho, faça
  se vetor[j] < vetor[minimo], então
   minimo $\leftarrow{}$ j
  fim-se
 fim-para
 temp $\leftarrow{}$ vetor[i]
 vetor[i] $\leftarrow{}$ vetor[minimo]
 vetor[minimo] $\leftarrow{}$ temp
fim-para

tamanho = comprimento do vetor

Funcionamento

A idéia é sempre procurar o menor elemento do vetor e inseri-lo no início do vetor. Procuramos o menor valor do vetor e colocamos ele em vetor[1]. Procuramos o menor valor do vetor excluindo o já colocado e colocamos ele em vetor[2]. E assim vamos indo até termos todo o vetor ordenado.

Partindo sempre a partir do último elemento reordenado (a partir do i), o programa procura o menor elemento no vetor e o substitue pelo elemento i atual.

Exemplo de Funcionamento

O programa recebe o seguinte vetor.

Aí ele começa com $i=1$. Vou sempre marcar $i$ com a cor preta e $min$ com a cor cinza.

Ele marca o próprio índice i como a variável minimo, que é sempre o menor elemento do vetor. Então, ele faz um para de $j=2$ até o comprimento do vetor, com o objetivo de descobrir qual o menor elemento.

$j=2$ … $v[j] = 3 < v[minimo] = v[1] = 5$, portanto $minimo = j = 2$.

$j=3$ … $v[j] = 3 < v[minimo] = v[1] = 5$, portanto $minimo = j = 2$.

$j=3$ … $v[j] = 7 > v[minimo] = v[2] = 3$, portanto não mexemos em nada.

$j=4$ … $v[j] = 8 > v[minimo] = v[2] = 3$, portanto não mexemos em nada.

$j=5$ … $v[j] = 2 < v[minimo] = v[2] = 3$, portanto $minimo = j = 5$.

$j=6$ … $v[j] = 2 < v[minimo] = v[2] = 3$, portanto $minimo = j = 5$.

$j=6$ … $v[j] = 5 > v[minimo] = v[5] = 2$, portanto não mexemos em nada.

Agora substituímos o v[minimo] pelo v[i], formando com isto o novo vetor:

E assim vamos fazendo com os outros elementos até que todo o vetor esteja ordenado.

Custo

Este algoritmo não tem um melhor/pior caso, porque todos os elementos são varridos, sempre. Medir seu custo é simples. Custo de linha por linha…

n = tamanho do vetor

1. $n$
2. $n$
3. $\sum\_{j=1}^{n} n$
4. $\sum\_{j=1}^{n} 1$
5. $\sum\_{j=1}^{n} 1$
6. $0$
7. $0$
8. $n-1$
9. $n-1$
10. $n-1$
11. $0$

Você pode estar se perguntando porque eu coloquei este custo para a linha 5. Afinal, a linha 5 diria que este programa tem um melhor/pior caso, porque ela não seria executada se o se retornar falso. Mas o caso é que ela é desprezível. Uma soma como estas para o custo geral do nosso algoritmo não vai influenciar em nada. Quer ver? Vamos somar os custos com esta linha valendo $0$ (como se nenhum se entrasse) e depois com ela valendo $\sum\_{j=1}^{n}$.

Primeiro cálculo

Segundo cálculo

Conclusão

Como vocês puderam ver, não faz diferença alguma o $\frac{n^{2} + n}{2}$ que aquela somatória nos proporciona. Já que todo o cálculo de algoritmos é baseado apenas no maior expoente de n e desprezamos todas as constantes (inclusive as que multiplicam o n de maior expoente, muitos passos são desprezíveis.

Também conhecida como Insertion Sort, a Ordenação por Inserção consiste em inserir um elemento $n$ num vetor já ordenado de $n-1$ elementos. Neste artigo, apresento-lhes este simples algoritmo para ordenação de vetores.

O pseudocódigo da ordenação por inserção é o seguinte:

para j $\leftarrow{}$ 2 até comprimento do vetor, faça
 elemento $\leftarrow{}$ vetor[j]
 i $\leftarrow{}$ j - 1
 enquanto i > 0 e vetor[i] > elemento, faça
  vetor[i + 1] $\leftarrow{}$ vetor[i]
  i $\leftarrow{}$ i - 1
 fim-enquanto
 vetor[i + 1] $\leftarrow{}$ elemento
fim-para

Para explicar eu vou fazer uma coisa que sempre faço para corrigir meus algoritmos, fingir que sou o programa, executando cada passo manualmente (claro que geralmente faço mais rápido, porque não preciso escrever tudo que faço). Vamos iniciar com o seguinte vetor v.

Aí o código me manda começar com $j=2$ e iterar até o comprimento do vetor (6). A primeira ordem que ele me dá é para armazenar o elemento $a[j]$ ($a[2]$) na variável elemento. Para facilitar toda a explicação eu vou sempre pintar de cinza o $v[j]$ onde eu estou (no caso, o segundo elemento do vetor, 3) e de preto o vetor ainda não ordenado (elementos $\geq{}j$).

Então ele me diz que $i \leftarrow{} j-1$. Portanto, $i=1$. E agora ele me faz um enquanto (que poderia ser substituído por para) onde meu i deverá ir diminuindo. Vamos entrar no loop…

Bom, meu $i = 1$ é maior que 0. $v[1]=5$ é maior que o $elemento=3$? Sim, então vamos entrar no corpo do enquanto… Aqui ele me manda fazer um $vetor[i+1] = vetor[i]$, que nesse caso é fazer um $v[2]=v[1]=5$.

E agora subtrai de i um valor. Portanto, $i=0$. Ele retorna ao enquanto, mas agora não satisfazemos a condição $i>0$, por isso saímos do enquanto. Então ele pede para $vetor[i+1]=elemento$ ($v[1]=elemento$). Portanto, o vetor fica assim:

E incrementamos o j, agora $j=3$.

$elemento = 7$

$i = 3-1 = 2$

$i > 0$… E $5 > 7$? Não! Portanto, não entramos no enquanto.

$v[3] = elemento$ (nenhuma mudança)

E lá vamos para $j=4$ e continuando até que vamos ter o vetor ordenado:

Qual a lógica?

Como eu já disse na introdução, mas lá sem grandes explicações, a Ordenação por Inserção divide o vetor em dois. O primeiro (de elementos $< j$) contém todos seus valores ordenados e o segundo (de elementos $\geq{} j$) contém os valores que devem ser inseridos no primeiro vetor já ordenado (por isso ele se chama Algoritmo de Inserção). A chave do algoritmo é o enquanto que acontece para ir deslocando todos os elementos para seu índice $+1$) contém todos seus valores ordenados e o segundo (de elementos $\geq{}j$) contém os valores que devem ser inseridos no primeiro vetor já ordenado (por isso ele se chama Algoritmo de Inserção).

A variável elemento só serve para não perdermos o valor de $v[j]$ (porque depois fazemos $v[i+1]=v[i]$ quando $i=j-1$)

Acredito que não tenham restado dúvidas. Dê mais uma olhada no algoritmo e tente implementar. Se tiver dificulade, coloque mensagens de debug estratégicas para entender o algoritmo. (ex.: no início do para coloque para imprimir o valor de j e no início de cada enquanto coloque para imprimir os valores elemento, i e v[i])

Custo

Você deve ter percebido que este algoritmo não tem um custo fixo. Se todo o vetor estiver ordenado, ele nunca precisará iterar o $i$ e portanto será executado bem mais rápido do que se o vetor estiver inteiro em ordem decrescente (quando ele sempre precisará iterar $i$ até o fim - 0). Então, neste artigo, gostaria-lhes de apresentar a análise de algoritmos baseada em casos. Para este programa, dizemos que:

• Melhor caso é quando todos os elementos já estão ordenados. Custo: $\Theta{}(n)$
• Pior caso é quando os elementos estão em ordem decrescente. Custo: $\Theta{}(n^{2})$

Em alguns programas o caso médio é importante também, mas não é o caso da ordenação por inserção. Vemos que há uma diferença bem grande entre o custo dos dois casos. Por isso, precisamos conhecer onde que nosso algoritmo será implementado e quais as chances de ele ser o melhor ou pior caso. Em geral, o pior caso é o mais comum… Por isso, diremos que o custo deste algoritmo é $\Theta{}(n^{2})$.