Há alguns meses, muitos administradores de páginas no Facebook reclamaram pela internet que suas páginas estavam começando a levar bem menos visitantes para os seus sites do que de costume. Em alguns casos, as entradas via Facebook teriam caído pela metade, mesmo com a quantidade de curtidas crescendo bastante.

Na época, comentou-se que essa queda no tráfego coincidiu com um novo recurso da rede social chamado “posts promovidos”, através do qual as empresas podem pagar ao Facebook para colocarem o seu conteúdo no feed de notícias de mais usuários.

A coincidência dos eventos fez com que parecesse que o Facebook estivesse artificialmente diminuindo o tráfego das páginas para ganhar dinheiro forçando seus donos a usarem o recurso de posts promovidos para voltarem a ter a quantidade de visitas que tinham anteriormente.

Porém, o Facebook insistiu que não estava fazendo nada do tipo. Ele estaria apenas tentando manter os feeds dos usuários sem tantos posts promocionais (que os usuários não gostariam de ver). Em outras palavras, a empresa de Mark Zuckerberg disse que está do lado dos usuários contra os anunciantes, embora esteja ganhando dinheiro no negócio.

Desculpa esfarrapada

Se o objetivo de fazer os posts de páginas serem menos visualizados era tornar o Facebook com menos posts de empresas e mais de pessoas, por que ao mesmo tempo criaram os posts promovidos? Se a empresa está disposta a investir dinheiro para fazer seu post ser visualizado, então tudo bem incomodar o usuário? E como ficam as páginas que não são de empresas, mas de organizações e comunidades que não têm dinheiro para investir na divulgação de posts?

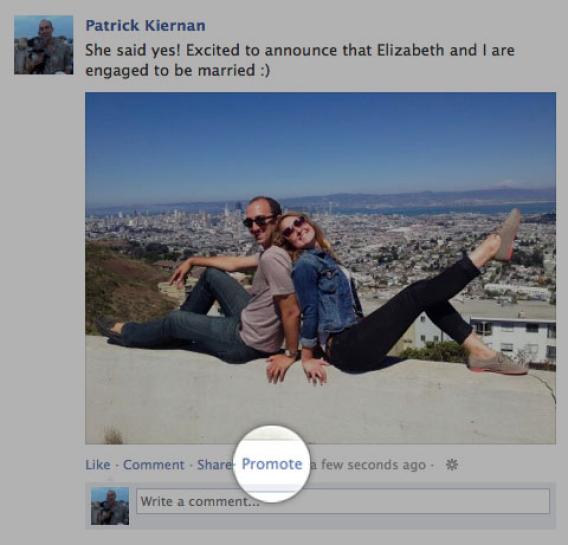
As contradições foram se acumulando e há cerca de um mês tivemos outra novidade: o Facebook começou a liberar o recurso de promover posts não só mais para páginas (empresas, anunciantes), mas também para usuários “normais” (eu e você). Nos últimos dias, mais e mais usuários no Brasil têm tido acesso ao botão Promote nas suas atualizações de status. As atualizações promovidas certamente tomarão cada vez mais espaço das atualizações que você gostaria realmente de ver na sua rede social. Como fica aquela velha desculpa?

Computação vs. Dinheiro

Em geral, o que decide se o que publicamos no Facebook aparece ou não para cada um dos nossos amigos é um algoritmo chamado EdgeRank (se quiser saber mais, dê uma olhada neste site, em inglês) que avalia basicamente nosso grau de afinidade, a interação de outras pessoas com a publicação e há quanto tempo ela foi feita. Critérios computacionais razoáveis para não encher seu feed com zilhões de atualizações irrelevantes. De fato, estima-se que seus posts cheguem a apenas 12% dos seus amigos.

Com a mudança, criou-se uma variável (nada computacional) a mais aí nesse algoritmo: o dinheiro que o usuário tem e está disposto a pagar para promover sua publicação. A defesa do Facebook baseia-se no fato de que com o algoritmo tradicional pessoas com quem você não interage normalmente poderiam não ficar sabendo de uma notícia importante que você gostaria que todos ficassem sabendo como um casamento ou uma gravidez. A princípio, o argumento parece fazer sentido, mas a interação numa notícia como essas não deveria já aumentar o EdgeRank suficientemente para ela aparecer para todos os seus amigos? Se não aumenta, por que ficar com a solução fácil? Talvez o algoritmo devesse ser repensado. Faz sentido encontrar atualizações de status que não são relevantes para mim simplesmente porque um amigo virtual pagou para me mostrar?

Facebook na contramão da democracia

A lógica dos posts promovidos é a lógica dos anúncios da TV. Em vez de resolver problemas de ranqueamento com inteligência, inventa-se a variável dinheiro. Sua opinião é mais importante simplesmente porque você tem um megafone e os outros não.

O argumento do Facebook não gerou grandes polêmicas porque ele funciona dentro da mesma lógica que estamos acostumados a ver o mundo funcionar. Mas esse modo de pensar não deve parecer natural.

A internet é um meio de comunicação inovador e com potencial revolucionário por causa de suas características descentralizadas e democráticas, completamente opostas aos meios de comunicação que a mídia tradicional utiliza.

Posts promovidos podem parecer pequenos detalhes sem importância. Porém, pensar na utilidade de um recurso como esse na rede social mais utilizada do planeta (que tem cumprido papel tão importante em grandes mobilizações sociais) é muito importante para conhecermos seus limites. O convite a blogar ganha um novo argumento.

Tabelas de preços de impressão são interessantes. É muito comum que quanto mais você imprima mais baratas as impressões fiquem, fazendo com que o gráfico de preço por impressões não seja monótono (isso é, você não necessariamente pague mais por um número maior de impressões).

Isso torna as gráficas boas candidatas de lugares para pensar em gráficos de funções de primeiro grau, assim como a busca binária é uma boa candidata de aplicação para pensar sobre logaritmos.

Hoje fui imprimir uma partitura e me deparei com a seguinte tabela:

Cópias	Preço
De 01 a 03 unidades	R$ 0,70 cada
De 04 a 10 unidades	R$ 0,50 cada
De 11 a 20 unidades	R$ 0,40 cada
De 21 a 50 unidades	R$ 0,30 cada
De 51 a 100 unidades	R$ 0,25 cada
Acima de 100 unidades	R$ 0,20 cada

(registrada em uma foto de um bilhão de dólares)

Se desenharmos um gráfico de preço (eixo y — vertical) por número de impressões (eixo x — horizontal), temos:

Observando esse gráfico (feio), percebemos que há alguns números de impressões que economicamente não faz sentido fazer. Por exemplo, 3 impressões custam R$ 2,10 enquanto 4 impressões custam R$ 2,00. 20 impressões custam R$ 8,00 enquanto 21 impressões custam R$ 6,30. 100 impressões custam R$ 25,00 enquanto 101 impressões custam R$ 20,20.

Mas não só esses. Os valores que não faz sentido imprimir no gráfico são todos aqueles cujo existe algum ponto a direita na mesma altura ou mais baixo, ou seja, todos os que pintei de amarelo:

Um problema econômico interessante para quando se está numa gráfica imprimindo é, portanto, descobrir quando estamos nos pontos amarelos. É interessante porque, se estivermos nos pontos amarelos, podemos aproveitar para imprimir mais cópias ou pedir ao dono da gráfica um desconto. Afinal, é razoável esperar que o preço que a gente pague seja limitado por este gráfico:

Descobrir se estamos numa região amarela é simples. Basta calcular o preço que pagaríamos a princípio (multiplicar o número de cópias pelo preço por cópias da região em que estamos) e comparar com o preço que pagaríamos se pedíssemos o menor número de cópias da região imediatamente mais barata. Por exemplo, faz sentido imprimir 15 cópias porque $15 \times 0.40=6.00$ é menor do que $21 \times 0.30 = 6.30$, mas não faz sentido imprimir 85 cópias porque $85 \times 0.25 = 21.25$ é maior do que $101 \times 0.20 = 20.20$.

---

Agora vamos inverter o problema. Vamos supôr que você é a gráfica e quer evitar esse tipo de cliente insuportável, fazendo o preço ir ficando mais barato proporcionalmente com o número de impressões, mas mantendo a função monótona (crescendo).

Poderíamos pensar em funções que crescem cada vez mais devagar…

… mas parece complicado achar uma função que não nos dê prejuízo quando o cliente quiser muitas cópias e parece especialmente complicado explicar para o cliente que o preço de x cópias é um monte de constantes multiplicadas pelo logaritmo de x.

Então talvez seja melhor pensar em funções de primeiro grau mesmo.

Se você separar todas as funções que encontramos na tabela de preços do problema anterior e colocá-las num gráfico, você vai ver que a interseção delas só acontece num ponto: o ponto x = 0.

(esse gráfico foi um oferecimento Wolfram Alpha)

Uma forma de resolver o problema é fazer com que as interseções sejam nos pontos onde o preço das impressões muda. Isso se faz movendo cada uma das funções um pouquinho pra cima, isso é, adicionando constantes às funções de primeiro grau.

Por exemplo: 3 cópias custam R$ 2,10. Se a partir de 4 cópias quisermos que as cópias custem R$ 0,50 em vez de R$ 0,70, podemos forçar que 4 cópias custem R$ 2,10 + R$ 0,50 = R$ 2,60. R$ 2,60 é R$ 2,00 + R$ 0,60. Logo, em vez de usarmos a função de preço $f(x) = 0.5x$ para $x$ entre 4 e 10, podemos usar a função $f(x) = 0.5x + 0.6$.

Se repetirmos o mesmo raciocínio para as outras interseções, a tabela de preços final fica assim:

Cópias	Preço
De 01 a 03 unidades	R$ 0,70 cada
De 04 a 10 unidades	R$ 0,60 fixo + R$ 0,50 cada
De 11 a 20 unidades	R$ 1,60 fixo + R$ 0,40 cada
De 21 a 50 unidades	R$ 3,60 fixo + R$ 0,30 cada
De 51 a 100 unidades	R$ 6,10 fixo + R$ 0,25 cada
Acima de 100 unidades	R$ 11,10 fixo + R$ 0,20 cada

(Isso aqui é só um exercício. Por favor, não façam isso, donos de gráficas!)

Agora note que as coisas passam a fazer mais sentido (embora muito mais caras):

• 3 cópias custam R$ 2,10 e 4 cópias custam R$ 2,60;
• 10 cópias custam R$ 5,60 e 11 cópias custam R$ 6,00;
• 20 cópias custam R$ 9,60 e 21 cópias custam R$ 9,90;
• 50 cópias custam R$ 18,60 e 51 cópias custam R$ 18,85;
• 100 cópias custam R$ 31,10 e 101 cópias custam R$ 31,30.

O gráfico monótono (e bonito) comprova:

Imagine-se num prédio de 100 andares com várias bolas. A partir de um determinado andar (desconhecido), quando você joga uma bola pela janela, a bola quebra. Você quer determinar precisamente qual é esse andar e a única coisa que pode fazer é jogar bolas de andares diferentes.

Se você tem muitas bolas e não se importa em quebrar quantas forem necessárias, você pode realizar uma busca binária. Uma busca binária, para começar com um exemplo, é aquilo que você faz naquele diálogo clássico:

— Pense num número de 1 a 100 e eu vou tentar adivinhar. A cada palpite, você precisa me dizer se o número que você pensou é maior ou menor do que meu chute.
— Pensei.
— 50
— Maior.
— 75
— Menor.
— 63
— Menor.
— 57
— Menor.
— 54
— Menor.
— 52
— Menor.
— 51
— Acertou!

A cada passo numa busca binária você divide o intervalo de possibilidades por dois. Você descarta metade dos números que poderiam ser a solução. Por isso, mesmo que você pense num número de 1 a 1.000.000.000 (um bilhão) eu certamente não vou demorar mais de 30 (isso é, logaritmo de um bilhão na base dois) tentativas para acertar exatamente o número que você pensou.

Por que logaritmo de um bilhão na base dois? Como eu comentei anteriormente, a cada número que eu chuto e você diz se é maior ou menor do que o resultado eu corto meu intervalo por dois. Portanto, o número de chutes necessários (no pior caso) é precisamente a quantidade de vezes que preciso dividir um bilhão por dois até chegar a um (até sobrar um único número possível para eu chutar, que necessariamente vai ser o número que você pensou).

$$1000000000 / 2 / 2 / \cdots / 2 = 1$$

Nosso problema é encontrar quantos 2 tem aí. Dividir um número por 2 k vezes é o mesmo que dividir por $2^k$. Logo, nosso problema é encontrar quanto vale k:

$$\frac{1000000000}{2^k} = 1$$

Multiplicando os dois lados da igualdade por $2^k$, temos:

$$1000000000 = 2^k$$

Tirando o logaritmo na base 2, concluímos:

$$\log_2 1000000000 = k$$

Ou seja, o logaritmo de n na base 2 é o número de vezes que precisamos dividir n por 2 para chegar em 1. Voltando ao problema inicial, como $log_2 100 < 7$, precisaremos jogar no máximo 7 bolas para determinar a partir de qual andar a bola quebrar. Quando você jogar uma bola, se ela quebrar é a mesma coisa que o seu amigo que pensou num número dizendo “O número que eu pensei é menor.” Se ela não quebrar, é equivalente ao seu amigo dizendo “O número que eu pensei é maior.”

Realizando uma busca binária, o pior caso (aquele caso no qual quebraremos mais bolas – e que jogaremos a maior quantidade de vezes) é quando a bola quebra no primeiro andar. Você joga as bolas dos andares 50 (poft!), 25 (poft!), 13 (poft!), 7 (poft!), 4 (poft!), 2 (poft!), 1, jogando um total de 7 e quebrando um total de 6 bolas.

Nada muito novo para quem já conhecia busca binária. Por isso, vamos modificar o problema: Suponha que você não tenha quantas bolas desejar, mas apenas duas bolas. Quando uma bola cai sem quebrar, você pode descer, pegá-la e jogá-la de novo. Qual a menor quantidade de vezes que você vai ter que jogar a bola para com certeza determinar a partir de qual andar as bolas começam a quebrar?

Fazer uma busca binária não funciona mais. No caso de a bola quebrar a partir do primeiro andar, assim que você joga uma bola do andar 50 (uma bola quebra) e outra do 25 (outra bola quebra), você não tem mais bolas e não tem ideia de qual é o andar a partir do qual as bolas começam a quebrar (tudo o que você sabe é que é algum andar entre 1 e 25).

Como usar as duas bolas para determinar exatamente o andar a partir do qual as bolas começam a quebrar jogando as bolas a menor quantidade possível de vezes? Qual é essa quantidade mínima de vezes que será necessário jogar bolas pela janela?

Obrigado ao David por ter me apresentado o problema. A solução é bem legal!

Editado para ficar mais claro: A quantidade mínima que queremos é a do pior caso, isso é, a menor quantidade de vezes que será necessário jogar a bola independente de qual for o andar. Por exemplo, suponha que eu jogue uma bola do andar 5 e não quebre. Aí eu jogue do andar 10 e não quebre. Do 15 e não quebre. E assim sucessivamente (de 5 em 5) enquanto ela não quebrar. Quando ela quebrar, eu pego a outra bola e jogo no último valor que eu joguei menos 4, menos 3, menos 2 e menos 1. O pior caso para esse algoritmo é quando a bola quebrar a partir do andar 99. Jogarei nos andares 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100 (poft!), 96, 97, 98, 99 (poft!), ou seja, 24 vezes. (Mas é possível usar um algoritmo mais esperto que isso: a resposta do problema é menor que 24.)

Editado para programadores: A generalização deste problema (para n andares em vez de 100 e k bolas em vez de 2) caiu na OBI 2010 (o problema se chama Altas Aventuras) e está no SPOJ para quem quiser resolver: ALTAS2. Quem me contou foi o André.

O crescimento da internet em todo o planeta expressa a necessidade da nossa geração de experimentar meios de comunicação diferentes dos que a mídia tradicional nos propõem. A sociedade é cada vez mais dependente dessa rede, que conecta as pessoas das mais distantes localidades em tempo real.

A internet não é a mesma de dez anos atrás. Uma conexão hoje é condição necessária para a utilidade de um computador e a rede está cada vez mais presente em diferentes dispositivos, em especial nos celulares. A web é hoje o espaço das aplicações e dos serviços: um espaço virtual aparentemente infinito para onde você faz upload de toda a sua vida. Você usa a internet para ouvir músicas, baixar filmes, editar documentos, conversar com amigos, pagar contas, planejar viagens, organizar calendário, ver mapas, guardar fotos, entre muitos outros usos. Porém, o principal deles continua sendo compartilhar, ou seja, difundir ideias.

Compartilhar sempre foi o cerne da internet. Desde a criação dos primeiros sites pessoais, passando pelos blogs e por ferramentas que auxiliam a sua criação, chegando às mais diferentes ferramentas de redes sociais. Por isso, a disputa da rede é feita através das brigas em torno do compartilhamento: o que pode e não pode compartilhar, o anonimato necessário para compartilhar verdades inconvenientes, a neutralidade dos serviços contra o filtro do que passa e não passa pela rede.

Por um lado, temos aqueles que defendem uma internet mais restrita e com menos liberdade, isso é, com mais cara de TV. A censura do Wikileaks, juntamente com a perseguição a Julian Assange, e os projetos de lei SOPA/PIPA (EUA), Sinde (Espanha), Lerras (Colômbia) e Azeredo (Brasil) foram os casos que mais chamaram atenção nos últimos tempos.

Por outro lado, tecnologias estão sendo construídas e superadas em tempo recorde para tornar o compartilhamento mais fácil. Os levantes recentes no Oriente Médio demonstraram a eficácia da internet em ajudar ativistas políticos e sociais a organizarem protestos, disseminarem informações para o público e enviarem notícias de prisões e repressões ao restante do mundo. Do ponto de vista da tecnologia, o Facebook, pela sua capilaridade, é hoje a maior expressão da internet de curtir e compartilhar.

A rede de Mark Zuckerberg teve papel destacado em importantes acontecimentos sociais e políticos do ano passado. Há vários exemplos. Organização e divulgação dos protestos que culminaram na queda de Hosni Mubarak no Egito. Construção do movimento 15-M da juventude da Espanha e de outros movimentos de indignados por todo o planeta. Surgimento do movimento Occupy Wall Street nos EUA. Aqui no Brasil, difusão de diversos atos contra o aumento da passagem de ônibus, Marcha da Liberdade, Marcha das Vadias, Fora Ricardo Teixeira, entre outros.

A internet de hoje não é a mesma do ano passado. Pelo seu funcionamento democrático e pela sua dimensão global, ela muda muito rápido. Por isso, cabe a nós experimentar o tempo todo novas formas de explorar o ciberespaço para aproveitar todo o seu potencial viralizante e discutir ideias que nos auxiliem na construção de instrumentos de mudança social que organizem mais e mais pessoas ao redor do mundo.

Embora o Facebook seja uma ferramenta de utilidade incontestável, sua hegemonia tem me preocupado. Não pelo motivo que sempre leio por aí (o de estarmos compartilhando toda a nossa vida com uma empresa que não tem uma política de privacidade muito razoável), mas principalmente por outros dois: seu caráter efêmero e seus algoritmos que nos separam em bolhas.

Achar algo que você leu no mês passado no Facebook é um pesadelo. Ainda que você lembre quem foi que compartilhou ou em que grupo, você precisa andar e andar na barra de rolagem até fazer seu cooler começar a gritar de tanto processamento de JavaScript para encontrar o que você queria. No caso de querer encontrar comentários ou uma coisa que você não lembra quem foi que postou, é difícil até imaginar por onde começar. Os posts do Facebook não são indexados por sites de busca e suas mensagens vão ficando sufocadas embaixo de uma pilha que cresce quanto mais você usa a rede social. Por mais que exista a tentativa da linha do tempo para você navegar por anos e meses, é inegável que o Facebook é a rede social do que está acontecendo e não do que aconteceu.

Além disso, sua rede de amigos no Facebook é muito limitada. Primeiramente porque você só pode ter 5000 amigos (mais assinantes, é verdade), mas principalmente porque uma porcentagem muito pequena deles efetivamente vêem o que você posta. Vou dar um exemplo: De julho a outubro publiquei todos os dias atualizações de status sobre as eleições municipais no meu perfil divulgando as propostas dos meus candidatos. Na véspera das eleições, mandei e-mails e mensagens no Facebook para grande parte dos meus contatos pedindo voto neles. Várias pessoas ficaram felizes com a recomendação e disseram que até receberem a mensagem nem sabiam que eu estava envolvido na campanha do PSOL.

Faz sentido. O algoritmo do Facebook provavelmente seleciona postagens de temas que você se interessa (costuma postar, curtir, comentar, compartilhar) para você ler. Os posts sobre banana tendem a ser visualizados por quem gosta de banana. Aí você fica fazendo propaganda de bananas para seus amigos bananeiros. Bom para receber curtidas e melhorar sua auto-estima, ruim se você quer discutir as vantagens da banana com mais pessoas que não são do seu grupo de estudos sobre banana. Além de que tem um monte de gente que gosta de banana, mas nunca vai ver seus posts simplesmente porque não é seu amigo.

Passei os últimos anos escrevendo muito no Facebook. O Facebook certamente é uma ferramenta muito importante, mas estou convencido de que ele tem um potencial infinitamente maior se caminhar junto com a escrita de blogs. Posso citar pelo menos três motivos:

1. Os blogs divulgam mensagens menos efêmeras e com mais conteúdo. Por isso, são espaços mais adequados à formulação e ao registro de ideias (que certamente não devem deixar de ir para as redes sociais para serem disseminadas nas bolhas).
2. Os blogs são indexados pelo Google. Com isso, aparecem nos resultados das buscas de quem se interessa pelas coisas que escrevemos e seus links fortalecem os sites que queremos difundir para o mundo através do aumento do seu pagerank.
3. Os blogs não só enviam mensagens, mas iniciam conversações. Posts em blogs geram não só reflexões, mas comentários, posts em outros blogs e discussões nas redes sociais.

Tenho uma rede de amigos que escreve coisas muito legais nas redes sociais. Debate os temas da atualidade, formula política, faz críticas inteligentes sobre uma porção de assuntos relevantes. Há muitas (bilhões, eu diria) pessoas que não leio no Facebook, que talvez leiam este post e que certamente também têm muito a contribuir para o saudável debate de ideias que precisamos travar o tempo todo para mudarmos as pessoas e mudarmos o mundo. Esses comentários merecem e precisam superar as fronteiras dos algoritmos do Facebook para gerar mais discussão e influenciar outras pessoas. Por isso, escrevo para fazer o convite: escreva um blog e compartilhe suas ideias!

Tem um blog? Compartilhe um link dele nos comentários.

No início de 2005, logo antes de começar o Ensino Médio, eu escrevi meu próprio sistema de blog (tipo pra concorrer com o WordPress — só que não) e comecei a blogar no endereço tableless.tiagomadeira.net. Estava empolgado com a ideia de construir uma web semântica, com XHTML e com tableless. Foi um pouco antes do “estouro” da blogosfera que veio com o ascenso do WordPress mais pro final do mesmo ano e pelos dois anos seguintes.

Desde lá e durante todo o ensino médio, eu bloguei muito. No final de 2005, o blog se transformou num WordPress e assumiu o endereço tiagomadeira.net. Além disso, no verão de 2005 para 2006 escrevi um blog-curso de algoritmos para estudar para a Olimpíada de Informática.

Um ano depois, comecei a escrever outro blog em parceria (o Mal Vicioso, com a Carol). E em 2007, passei a participar timidamente ainda de outro (o 1001 Gatos de Schrödinger, do Ibrahim).

Em 2008, quando entrei na UFSC, fiquei um ano completamente sem blogar. Foi provavelmente o meu ano mais longe da internet, devido ao estudo sério de matemática e o treinamento intensivo para a Maratona de Programação (foi nesse ano que nossa equipe se classificou para a final mundial na Suécia).

Quando vim para São Paulo, em 2009, resolvi voltar a blogar. Porém, depois de ter ficado um ano sem dar bola pro meu blog, não me senti confortável em continuar usando ele (além de que fui tentar organizá-lo e acabei perdendo conteúdo sem querer). Aí acabei criando outro no endereço blog.tiagomadeira.com.

O conteúdo do tiagomadeira.net acabou ficando jogado às traças num leiaute terrível com mais publicidade do AdSense do que conteúdo. A mesma coisa aconteceu com o blog de algoritmos, que curiosamente continuou sendo bem visitado (valeu, Google!). E os outros dois blogs (Mal Vicioso e 1001 Gatos) simplesmente morreram.

Vinha pensando há algum tempo em fazer alguma coisa para salvar o conteúdo de todos esses blogs. Até que nesse sábado resolvi botar a mão na massa e toquei esse meu projeto egocêntrico: Escrevi um novo design e exportei/importei os posts de todos os outros blogs para este novo, relendo os posts para corrigir formatação, imagens e links quebrados.

Estou inaugurando este blog com textos dos últimos oito anos, ou seja, que registram acontecimentos interessantes de mais de 1/3 do meu tempo de vida. Encontrei uma porção de coisas legais quando resgatava os posts: angústias, ideias, planos, descobertas. Definitivamente valeu a pena não permitir que isso tudo se perdesse no buraco negro da internet.

Acabei motivado a continuar escrevendo aqui para contar o que ando pensando e para que no futuro eu continue me divertindo com meus velhos projetos. Ansioso para ver se a motivação vai vingar.